# Projections and Coordinate Systems
The problem with maps is that no map is undistorted. Because a round (three dimensional) body , such as the Earth, is brought to a flat (two dimensional) surface distortions regarding shape, direction or distances are inevitable. Therefore, there is no perfect map projection. Different projections were established to serve certain purposes so some may be used for specific tasks and extends. Most national govermental agencies lay out what they use for their spatial data and product so it is a good way to figure out a projection that is used on larger scaled maps than world maps.
Problem of ANY map projection:
The geography inevitably distorts in any case!
Distortions refer to the exaggeration or falsification of Earth's true shape regarding shape, area or distance.
Therefore, even though hundreds of projections exist, none is a perfect resemblence of the Earth. Developer of map projections aim to minimize the distortion as much as possible, mostly at the expense of a growing distortion of other elements, e.g. of places outside the map or on the map with less significance.
Globes
The only correct representation of the surface can be found on a globe. Even though globes do not show distortions, they do have their drawbacks: their bulkiness makes it hard to measure and the map reader is not able to compare two places opposite of each other at the same time, as only one side of the globe at the time can be viewed.
# The Graticule of the Earth
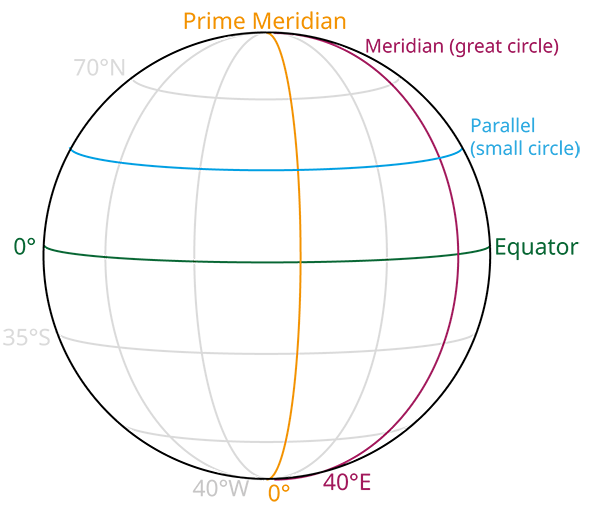
Using the two poles of the planet as its fixed points, a reference system can be established by using the connection of these points as the axis the planet rotates around.
A great circle divides the sphere in half through the center of the Earth. The equator is such a great circle and serves as a starting line as 0°. Depending on the direction, distances from the equator are measured in degrees to the north or south with a maximum of 90° - these distances are called latitude. Connecting all points of the same latitude creates a small circle around the sphere having the same angular distance from the equator, also referred as parallels. Great circles terminated by the poles connect all points of a given longitude and are orthogonal to the equator: meridians. Owing to a missing fixed point or line, a true origin at 0° is not given. However, after many years of country's usage of individual origin lines (runing through the country's capitol or other significant places) the international prime meridian was established in 1884 dividing the earth into east and west at Greenwich, England.
On a funny note: xkcd comic to map projections
# Azimuthal Projection
In an azimuthal projection the plane touches the earth at a tangent point. The lines intersecting with this point at an equal angle are great circles (usually meridians).
- Orthographic projections uses the projection point as infinite entity using projection lines orthogonal to the projetion plane. Shape and area are increasingly distorted the closer to the edge of the plane.
- Stereographic projections preserve the shapes and are therefore conformal. The projektion point is opposite of the plane's tangent point to the sphere.
- Gnomonic projections project maps from Earth's center displaying great circles as straight lines and only being able to present one hemisphere at a time. Distortion increase away from the projection point.
Azimuthal projections are extensifely used for polar regions or maps focused on a specific place only showing one side of the sphere.
| Projection Name | Notes | Example Image |
|---|---|---|
| Azimuthal Equidistant | 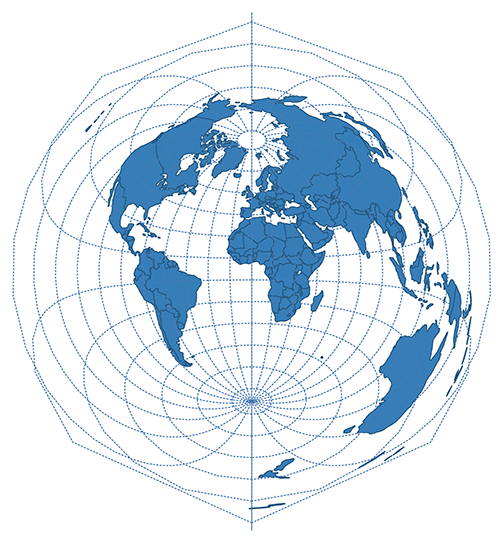 | |
| Lambert Azimuthal Equal Area | 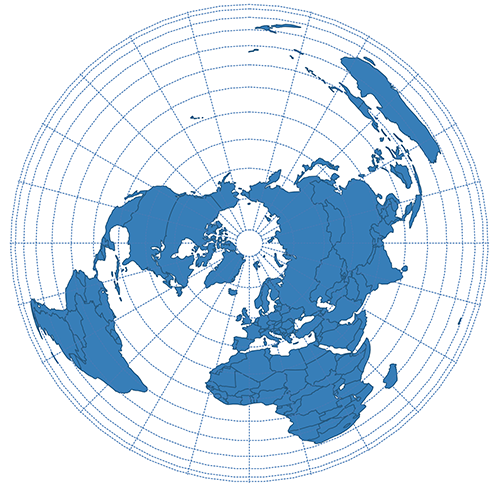 | |
| Polar Stereographic | 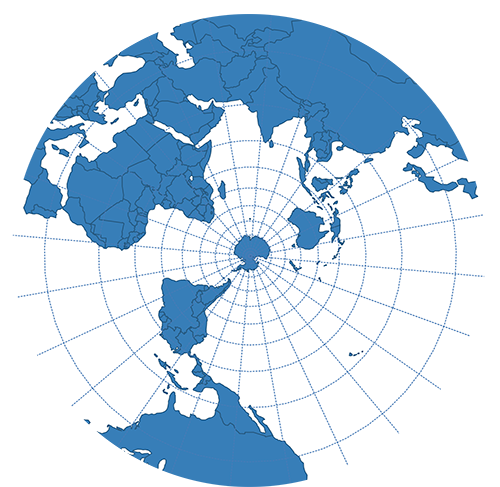 | |
| Gnomonic | 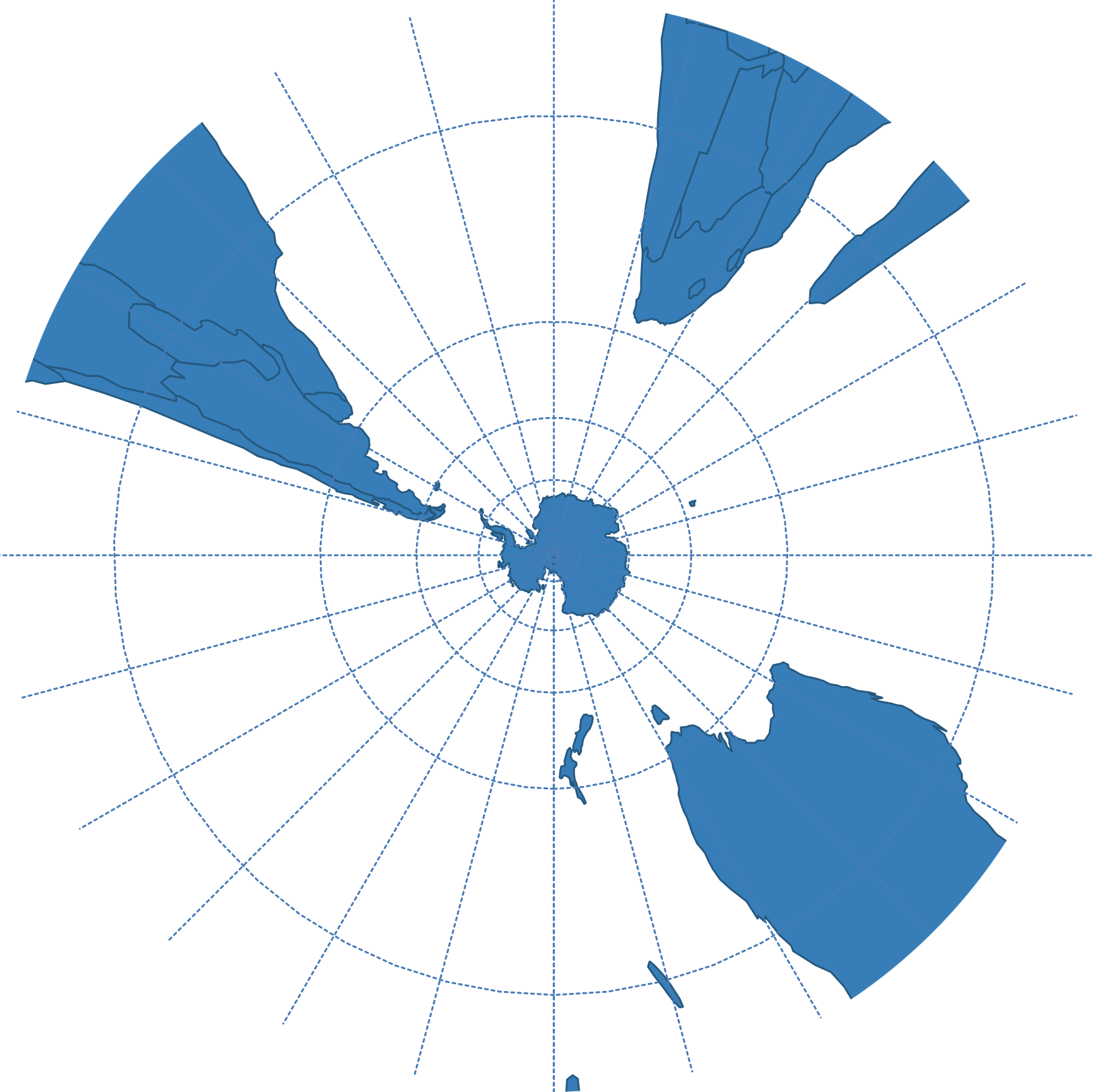 | |
| Winkel-Tripel | Pseudoazimuthal | 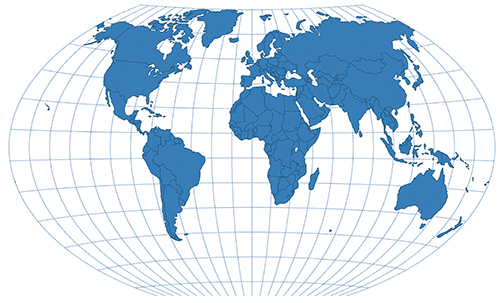 |
| Loximuthal | Pseudoazimuthal | 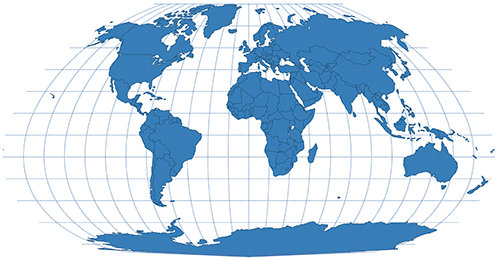 |
| Aitoff | Pseudoazimuthal | 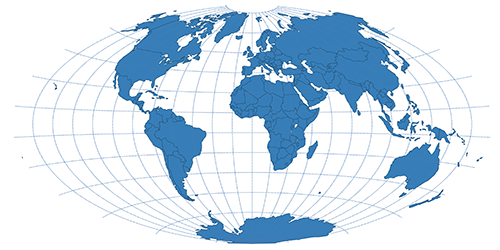 |
Pseudoazimuthal
Pseudoazimuthal projections can be identified by their grid: equator and central meridian are perpendicular and straight. Parallels are curves bowing towards the poles and away from the equator, meridians bow towards the central meridian in complex curves.
# Conic Projections
Conic projections create a map by setting a cone over a globe with a center point equal to the sphere's center. The cone's contact is tangent to a single latitude line, every other latitude is projected as rings. Meridians start at the cone's apex using any longitude line as a cut. The central meridian is then located directly opposite the cut line.
Typically used for mid-latitude zones with an east-west orientation, polar regions are often-times removed due to extreme distortion.
| Projection Name | Notes | Example Image |
|---|---|---|
| Lambert Conformal Conic | 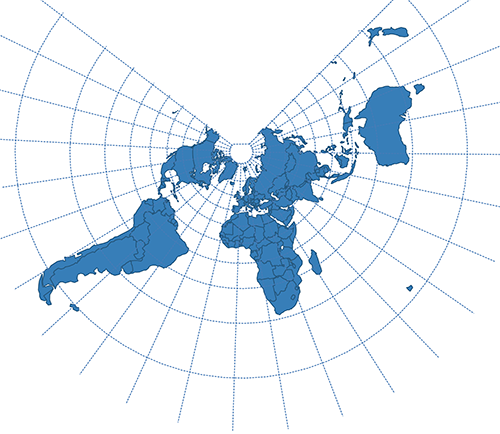 | |
| Albers Conic Equal Area | 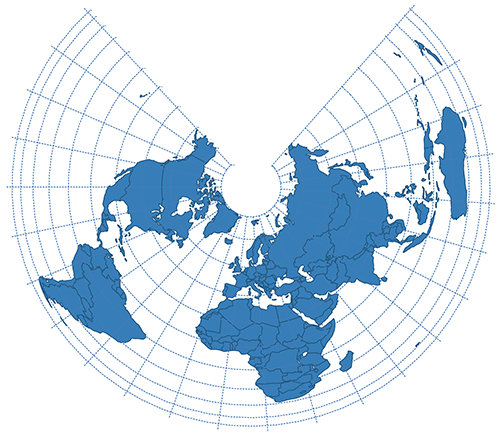 | |
| Bonne | Pseudoconic | 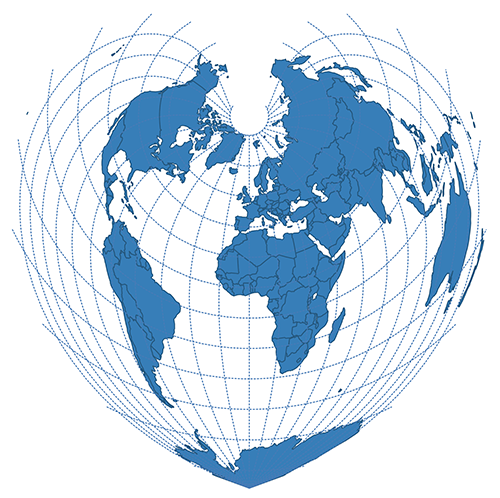 |
| Polyconic | Pseudocyndrical | 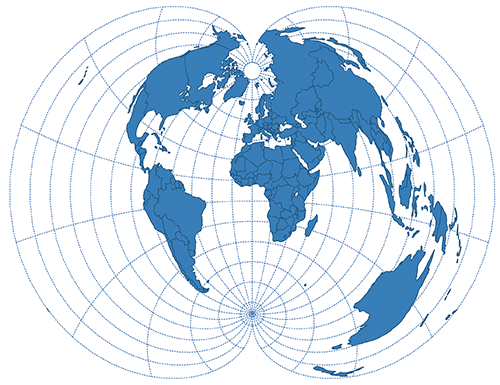 |
# Cylindrical Projections
The projection plane is cylindrically wrapped around the sphere which are either touching it by a great circle or secants it. The pojection is either conformal or equal-area.
| Projection Name | Notes | Example Image |
|---|---|---|
| Gall | 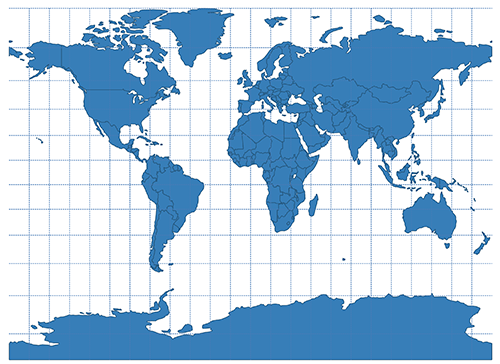 | |
| Cylindrical Equidistant Projection | 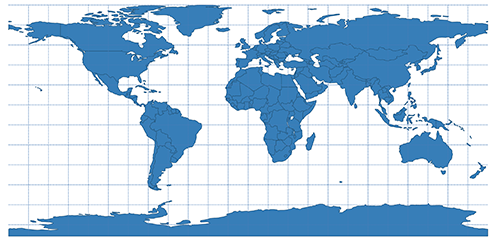 | |
| Robinson | Pseudocyndrical | 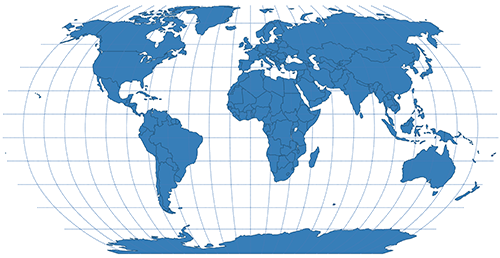 |
| Eckert IV | Pseudocyndrical | 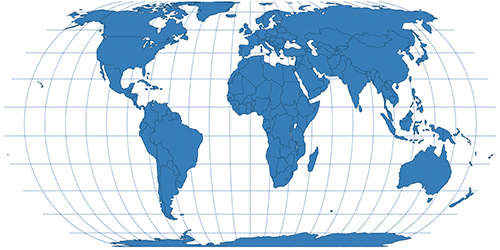 |
| Eckert VI | Pseudocyndrical | 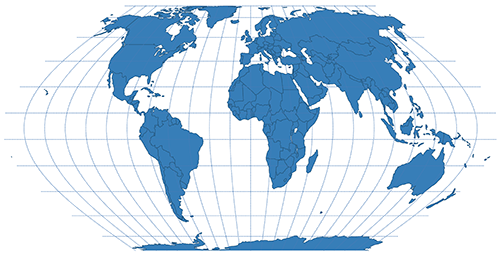 |
| Mollweide | Pseudocyndrical | 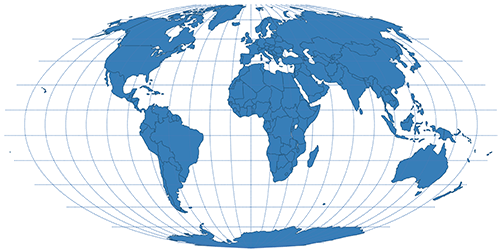 |
| Equal Earth | Pseudocyndrical | 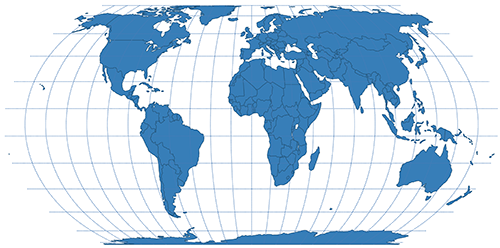 |
Pseudocylindrical
Pseudocylindrical projection can be identified by their grid, where longitude lines (except for the central meridian) are curved and evenly spaced along a straight latitude lines.
# Mercator
Mercator is probably the most famous projection and uses Earth's roration axis as the center axis of its cylinder, which touches the sphere at the equator. This projection is conformal.
Mercator is mostly useful for mapping regions close to the equator or marine charts (conformal).
# Transverse Mercator
Transverse Mercator map projection uses a cylinder rotated by 90° and touching along a longitude-line. Therefore, only equator and the tangent line (central meridian) are displayed as straight lines. Every other longitude and latitude are complex curves. The projection is used for regions with a north-south orientation (e.g. North & South America) and in UTM or Gauß-Krüger coordinate systems.
# Web-Mercator
The Web Mercator projection used in web maps is a rectangular projection and was also brought by Google Maps. While the distortions are insignificant on larger scales, the land masses on small scales are way out of proportions, owing to the fact, that the projection is using WGS84 geographical coordinates defined on a sphere, resulting in simpler and faster calculations. Other than the Mercator projection itself, the Web Mercator is technically non-conformal, even though a visual difference cannot be seen, which is important when displaying aerial imagery to avoid distortions of buildings. Contrarily, on a global scale, it is rather inefficient for visualizing thematic situations, as the Mercator projections distorts the land mass shapes immensely but is used by the majority of online map providers none the less.
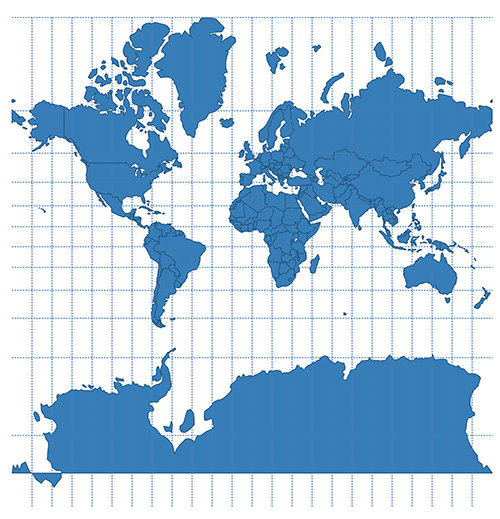
Because of the structure of map tiles (size usually being 256 by 256px), the map needs to be rectangular to be divided evenly into tiles so that a square aspect ratio is used at a maximal latitude of approx. 85.05 degrees. Another attribute of the projection is, that there are no special restriction: when zooming out of the OSM map it can be seen, that the map is repeated in west and east direction. The projection is also called Google Mercator (EPSG:900913),Spherical Mercator or Pseudo Mercator (EPSG:3857). Figure below shows the projection in combination with the Tissot’s Indicatrix to emphasize the distortion.
The true Size
To demonstrate how much distortion exists in well known web maps using Webmercator projection, such as Google Maps, check out the true size (opens new window) of countries.
Have a look at this beautiful, interactive website about Mercator and his maps: Mercator. It's a flat, flat world! (opens new window)
# Spilhaus projection
# EPSG
EPSG describes a database of coordinate reference information and tranformation established by European Petroleum Survey Group. The spatial references may be applied on global, regional, national or local scale.
Each entry in the EPSG database has a unique code associated with it. These codes are known as EPSG codes and they seem to be found everywhere that spatial data lurks. (Tom Roth)
Therefore, each coordinate reference can be identified by such an ESPG code, e.g. EPSG:3857 (opens new window), which is the code for Web Mercator.
EPSG codes not only refer to coordinate reference systems but can also hold information about datums, prime meridians, usage area, spheroids, ellipsoids and more.
# Choosing the right projection
| Area | Purpose | Projection |
|---|---|---|
| Whole World | Web map | Pseudo-Mercator |
| Whole World | Paper map | Robinson, Equal Earth, Miller |
| Continent | Thematic map | Lambert Azimuthal Equal Area |
| Oceans | Orthographic or Lambert Azimuthal Equal Area | |
| Polar Regions | Orthographic or Lambert Azimuthal Equal Area | |
| N-S Regions | e.g. Chile | Transverse Mercator |
| E-W Regions | e.g. USA | Lambert Conformal Conic |
TIP
For further reading have a look at Choosing a projection (opens new window) and Guide to Selecting Map Projections (opens new window).
# Overview
| Area | Georeferencing | EPSG Code |
|---|---|---|
| Europe | ETRS89 / LCC Europe | 3034 (opens new window) |
| Austria | MGI / Austria M28 | 31284 (opens new window) |
| Austria | MGI / Austria M31 | 31285 (opens new window) |
| Austria | MGI / Austria M34 | 31286 (opens new window) |
| Germany | Geographical coordinates in decimals: WGS84, ETRS89 | 4326 (opens new window), 4258 (opens new window) |
| Germany | DHDN / 3-degree Gauss-Kruger nth zone (zone 2 to 5), Bessel Ellipsoid | 31466 (opens new window) - 31469 (opens new window) |
| Germany | UTM Zone 32 and 33 without easting, Ellipsoid GRS80 | 25832 (opens new window), 25833 (opens new window) |
| Germany | UTM Zone 32 and 33 with easting, Ellipsoid GRS80 | 4647 (opens new window), 5650 (opens new window) |
| Germany | Lambert conformal conic projection, Ellipsoid WGS84 | 4839 (opens new window) |
| Great Britain | British National Grid | 27700 (opens new window) |
| Iraq | Iraq National Grid | 3893 (opens new window) |
| Netherlands | Amersfoort / RD New -- Netherlands - Holland - Dutch | 28992 (opens new window) |
| New Zealand | NZGD2000 / New Zealand Transverse Mercator 2000 -- New Zealand Transverse Mercator (NZTM) | 2193 (opens new window) |
| New Zealand | NZGD2000 Meridional Circuits | 4959 (opens new window) |
TODO
This part is under construction!
USA: State Plane Coordinate System, United States National Grid
New Zealand > see Land Information New Zealand: Projections (opens new window).
# Useful Tools
- Projection Wizard (opens new window) lets you define an area and suggests projections based on the selected area!
- This tool (opens new window) lets you find out the details of well known projections in an clear interactive overview.
- One of the biggest ressources for map projections is map-projections.net (opens new window) offering a tool to compare projections and see clear differences.
- Flex Projector (opens new window) is a freeware, cross-platform application for creating custom world map projections
# References
- Annoni, A., Luzet, C., Gubler, E., Ihde, J., 2003. Map Projections for Europe. Italy: European Communities. (online (opens new window), accessed 23 Oct 2019)
- Axis Maps. Map Projections (opens new window) (accessed 15 Aug 2019).
- Albrecht, J., 2005. Projection concepts used in the 4th GTECH 361 lecture (opens new window). (accessed 21 Oct 2019)
- Battersby, S. E., Finn, M. P., Usery, E. L. & Yamamoto, K. H., 2014. Implications of Web Mercator and Its Use in Online Mapping. Cartographica, Issue 49 (2).
- Dempsey, C., 2002. What is a Map Projection? (opens new window). (accessed 21 Oct 2019)
- Esri, 2000. Understanding Map Projections. Esri. (online (opens new window), accessed 23 Oct 2019)
- Geoawesomeness (2017). Which is the best map projection? (opens new window). (accessed 22 Aug 2019)
- ICSM. Commonly used Map Projections (opens new window). (accessed 23 Oct 2019)
- IDL Online Help. 2005. Map Projections (opens new window). (accessed 21 Oct 2019)
- Jansen, M. & Adams, T., 2010. OpenLayers - Webentwicklung mit dynamischen Karten und Geodaten. München: Open Source Press.
- Jung, T.. Was ist eine Kartenprojektion? – Eine kurze Einführung (opens new window). (accessed 21 Oct 2019)
- Kessler, F. C., Battersby, S. E., Finn, M. P. & Clarke, K. C., 2017. Map projections and the Internet. In: Choosing a map projection. s.l.:Springer, pp. 116-148.
- ICA Commission on Map Projections. Map Projections (opens new window). (accessed 21 Oct 2019)
- Manifold Software Limited, 2019. Guide to Selecting Map Projections (opens new window). (accessed 23 Oct 2019)
- Manifold Software Limited, 2019. National Grid Projections (opens new window). (accessed 23 Oct 2019)
- Muehlenhaus, I., 2014. Web Cartography. Boca Raton: CRC Press.
- Roth, T., 2017. EPSG Code explained (opens new window). (accessed 23 Oct 2019)
- Schwartz, J., 2018. Bing Maps Tile System (opens new window). (accessed 12 July 2018)
- Seidel, S., 2004. Infoblatt Kartenprojektionen (opens new window). Leipzig: Klett. Edited 2012. (accessed 21 Oct 2019)
- Snyder, J.P., 1987. Map projections- A working Manual. U.S. Geological Survey Professional Paper. 1395. Washington, D.C.: U.S. Government Printing Office. online (opens new window)
- Snyder, J.P, 1994. An Album of Map Projections. U.S. Geological Survey Professional Paper. 1453. Washington, D.C.: U.S. Government Printing Office. online (opens new window)
- Snyder, J.P., 1993. Flattening the Earth: two thousand years of map projections. Chicago: The University of Chicago.
- Tyner, J. A., 1992. Introduction to Thematic Cartography. New Jersey: Prentice-Hall Inc.
- https://en.wikipedia.org/wiki/Map_projection
- Azimuthal Projection: Orthographic, Stereographic and Gnomonic (opens new window). (accessed 21 Oct 2019)